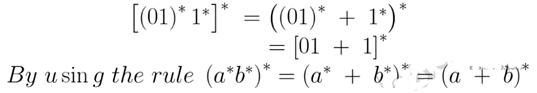Q1. A Turing Machine is an accepting device which accepts the languages __________.
(a) recursively enumerable set
(b) recursively set
(c) enumerable set
(d) none of the above
Show Answer
Answer : Option (A)
Q2. Let L={w∈(0+1)∗∣w has even number of 1's}, i.e. L is the set of all bit strings with
even number of 1's. Which one of the regular expression below represents L?
(a) (0∗10∗1)∗
(b) 0∗(10∗10∗)∗
(c) 0∗(10∗1∗)∗0∗
(d) 0∗1(10∗1)∗10∗
Show Answer
Answer : Option (B)
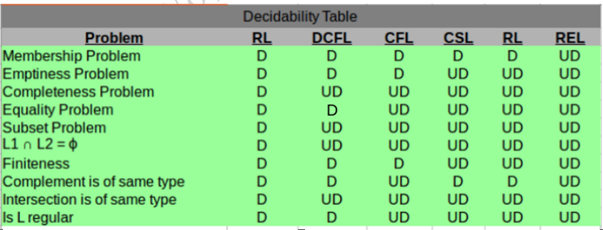
Q3. Which of the following problems are decidable?
(a) Does a given program ever produce an output?
(b) If L is a context-free language, then, is L also context-free?
(c) If L is a regular language, then, is L also regular?
(d) If L is a recursive language, then, is L also recursive?
Show Answer
Answer : Option ( C,D )
Explanation: CFL's are not closed under complementation. Regular and recursive
languages are closed under complementation.
Q4. Which of the following are decidable?
(a) Whether the intersection of two regular languages is infinite
(b) Whether a given context-free language is regular
(c) Whether two push-down automata accept the same language
(d) Whether a given grammar is context-free
Show Answer
Answer : Option (A, D )
Q5. Which of the following statements is false?
(a) The halting problem for Turing machine is un-decidable
(b) Determining whether ambiguity a context free grammar is un-decidable
(c) Given two arbitrary context free grammars G1 and G2 whether L(G1)=L(G2)
(d) Given two regular grammars G1 and G2, it is un-decidable whether
L(G1)=L(G2)
Show Answer
Answer : Option ( D )
Explanation:
Case (a): The Halting Problem for TM is un-decidable problem. By un-decidable means no
algorithm exist for it.
Case (b):Ambiguity in a CFG is undecidable. No algorithm can decide if a CFG is ambiguous. by ambiguous means the CFG has two or more derivations for some sentence.
Case (c):The equivalance problem of CFG's is undecideable. We have no algorithm to decide if
two CFG's generate the same language.
Case (d):The regular sets are a well behaved class of languages. Practically everything about
Regular Language is decidable.
Q6. Which one of the following problems is un-decidable?
(a) Deciding if a given context-free grammar is ambiguous.
(b) Deciding if a given string is generated by a given context-free grammar.
(c) Deciding if the language generated by a given context-free grammar is empty.
(d) Deciding if the language generated by a given context-free grammar is finite.
Show Answer
Answer : Option (A)
Q7. Which one of the following is the strongest correct statement about a finite language
over some finite alphabet ∑?
(a) It could be un-decidable
(b) It is Turing-machine recognizable
(c) It is a regular language
(d) It is a context-sensitive language
Show Answer
Answer : Option (C)
Q8. It is decidable whether:
(a) An arbitrary Turing machine halts after 10 steps.
(b) A Turing machine prints a specific letter.
(c) A Turing machine computes the product of two numbers.
(D) None of the above.
Show Answer
Answer : Option (A, C )
Explanation:
Case (a):Just run the TM for 10 steps and see it halts or not. So this is decideable.
Case (b):The printing problem of TMs is Undecidable. This can be reduce to the halting problem when the TM halts let it print something.
Case (c):Multiplication, Addition can be done by TM so this is decidable.
Q9. Which of the following problems are un-decidable?
(a) Membership problem in context - free languages.
(b) Whether a given context - free language is regular.
(c) Whether a finite state automation halts on all inputs.
(d) Membership problem for type 0 languages.
Show Answer
Answer : Option (B, D )
Q10. Which one of the following regular expressions correctly represents the language of
the finite automation given below?
(a) ab*bab* + ba*aba*
(b) (ab*b)* ab* + (ba*a)*ba*
(c) (ab*b + ba*a)* (a* + b*)
(d) (ba*a + ab*b)* (ab* + ba*)
Q11. Which one of the following regular expressions represents the set of all binary
strings with an odd number of 1’s?
(a) 10*(0*10*10*)*
(b) ((0 + 1)*1(0 + 1)*1)*10*
(c) (0*10*10*)*10*
(d) (0*10*10*)*0*1
Show Answer
Answer : Option (C)
Q12. Consider the following statements.
I. If L1 ∪ L2 is regular, then both L1 and L2 must be regular.
II. The class of regular languages is closed under infinite union.
Which of the above statements is/are TRUE?
(a) I only
(b) II only
(c) Both I and II
(d) Neither I nor II
Show Answer
Answer : Option ( D )
Q13. For Σ = {a, b}, let us consider the regular language L = {x | x = a^2+3k or x =
b^10+12k, k ≥ 0}. Which one of the following can be a pumping length (the constant
guaranteed by the pumping lemma) for L?
(a) 9
(b) 5
(c) 24
(d) 3
Show Answer
Answer : Option (C)
Explanation: According to the Pumping Lemma for Regular Languages, every string w
present in the infinite regular language L should be divide into three parts w = xyz, where
(i) y ≠ ε
(ii) |xy| ≤ n , where n is some positive integer and |w| ≥ n
(iii) for every i ≥ 0, the string xyiz is also in L.
From the question,
when x = b10+12k
then minimum possible string is = b10 or 'bbbbbbbbbb'.
we cannot divide this into three parts x, y, z.
So pumping length should must be more than 10 so that we can divide any string into
three parts.
Q14. If L is a regular language over Σ = {a,b}, which one of the following languages is
NOT regular?
(a) Suffix (L) = {y ∈ Σ* such that xy ∈ L}
(b) {wwR │w ∈ L}
(c) Prefix (L) = {x ∈ Σ*│∃y ∈ Σ* such that xy ∈ L}
(d) L ∙ LR = {xy │ x ∈ L, yR ∈ L}
Show Answer
Answer : Option (B)
Q15. Language L1 is defined by the grammar: S1→aS1b|ε
Language L2 is defined by the grammar: S2→abS2|ε
Consider the following statements:
P: L1 is regular
Q: L2 is regular
Which one of the following is TRUE?
(a) Both P and Q are true
(b) P is true and Q is false
(c) P is false and Q is true
(d) Both P and Q are false
Show Answer
Answer : Option (C)
Q16. The number of states in the minimum sized DFA that accepts the language defined
by the regular expression
(0+1)∗(0+1)(0+1)∗ is ___________________.
(a) 2
(b) 3
(c) 4
(d) 5
Show Answer
Answer : Option (A)
Q17. Which one of the following regular expressions represents the language: the set of
all binary strings having two consecutive 0s and two consecutive 1s?
(a) (0+1)∗0011(0+1)∗+(0+1)∗1100(0+1)∗
(b) (0+1)∗(00(0+1)∗11+11(0+1)∗00)(0+1)∗
(c) (0+1)∗00(0+1)∗+(0+1)∗11(0+1)∗
(d) 00(0+1)∗11+11(0+1)∗00
Show Answer
Answer : Option (B)
Q18. Let L be the language represented by the regular expression ∑∗0011∑∗ where ∑={0,1}. What is the minimum number of states in a DFA that recognizes L―(complement of L)?
(a) 4
(b) 5
(c) 6
(d) 8
Show Answer
Answer : Option (B)
Q19. The length of the shortest string NOT in the language (over ∑={a,b}) of the following regular expression is ____________.
a∗b∗(ba)∗a∗
(a) 1
(b) 2
(c) 3
(d) 4
Show Answer
Answer : Option (C)
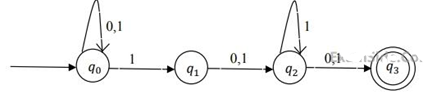
(a) {q0,q1,q2}
(b) {q0,q1}
(c) {q0,q1,q2,q3}
(d) {q3}
Show Answer
Answer : Option (A)
Q21. If L1={a^n|n≥0} and L2={b^n|n≥0}, consider
I) L1∙L2 is a regular language
II) L1∙L2={a^nb^n|n≥0}
Which one of the following is CORRECT?
(a) Only (I)
(b) Only (II)
(c) Both (I) and (II)
(d) Neither (I) nor (II)
Show Answer
Answer : Option (A)
Q22. Which one of the following is TRUE?
(a) The language L={anbn|n≥0} is regular.
(b) The language L={an|n is prime} is regular.
(c) The language L={w|w has 3k+1 b′ s for some k∈N with ∑={a,b}} is regular.
(d) The language L={ww|w∈∑∗ with ∑={0,1}} is regular.
Show Answer
Answer : Option (C)
Q23. Consider the languages L1=ϕ and L2={a}. Which one of the following represents
L1L2∗UL1∗?
(a) {ε}
(b) ϕ
(c) a∗
(d) {ε,a}
Show Answer
Answer : Option (A)
Q24. What is the complement of the language accepted by the NFA shown below?
Assume ∑={a} and ε is the empty string.
(a) ϕ
(b) {ε}
(c) a∗
(d) {a,ε}
Show Answer
Answer : Option (B)
Q25. Let L1 recursive language. Let L2 and L3 be languages that are recursively
enumerable but not recursive. Which of the following statement is not necessarily true?
(a) L2 − L1 is recursively enumerable.
(b) L1 − L3 recursively enumerable.
(c) L2∩L1 is recursively enumerable.
(d) L2∪L1 is recursively enumerable.
Show Answer
Answer : Option (B)
Q26. Which one of the following languages over the alphabet {0,1) is described by the
regular expression (0+1)∗0(0+1)∗0(0+1)∗
(a) The set of all strings containing the substring 00
(b) The set of all strings containing at most two 0′s
(c) The set of all strings containing at least two 0′s
(d) The set of all strings that begin and end with either 0 or 1
Show Answer
Answer : Option (C)
Q27. Consider the set ∑∗ of all strings over the alphabet ∑={0,1}.∑∗ with the concatenation operator for strings
(a) Does not from a group
(b) Forms a non-commutative group
(c) Does not have a right identity element
(d) Forms a group if the empty string is removed from
Show Answer
Answer : Option (A)
Q28. The regular expression 0∗(10∗)∗denotes the same set as
(a) (1∗0)∗1∗
(b) 0+(0+10)∗
(c) (0+1)∗10(0+1)∗
(d) None of the above.
Show Answer
Answer : Option ( D )
Q29. Given an arbitrary non-deterministic finite automaton (NFA) with N states, the maximum number of states in an equivalent minimized DFA is at least
(a) N^2
(b) 2^N
(c) 2N
(d) N!
Show Answer
Answer : Option (B)
Q30. Consider the following two statements;
S1:{0^2n|n≥1} is a regular language
S2:{0^m1^n0^m+n|m≥1andn≥1} is a regular language
Which of the following statements is correct?
(a) Only S1 is correct
(b) Only S2 is correct
(c) Both S1 and S2 are correct
(d) None of S1 and S2 is correct
Show Answer
Answer : Option (A)
Q31. Let L denote the language generated by the grammar S→0S0|00. Which one of the following is true?
(a) L=0+
(b) L is regular but not 0+
(c) L is context free but not regular
(d) L is not context free
Show Answer
Answer : Option (C)
Q32. Let S and T be languages over ∑={a,b} represented by the regular expressions
(a+b∗)∗ and (a+b)∗, respectively. Which of the following is true?
(a) S⊂T
(b) T⊂S
(c) S=T
(d) S∩T=ϕ
Show Answer
Answer : Option (C)
Q33. Consider the regular expression (0+1)(0+1).......n times. The minimum state finite automation that recognizes the language represented by this regular expression contains:
(a) n states
(b) n+1 states
(c) n+2 states
(d) None of the above
Q34. How many substrings of different lengths (non-zero) can be formed from a character
string of length n ?
(a) n
(b) n2
(c) 2n
(d) n(n+1)/2
Show Answer
Answer : Option ( D )
Explanation:
Example:
Let w = GAT be a string then |w|= 3
The substrings possible are = { ε,G,A,T,GA,AT,GAT}
So,the substring of length 0 = 1 { the string is = ε }
the substring of length 1 = 3 { the strings are = G,A,T }
the substring of length 2 = 2 { the strings are = GA,AT }
the substring of length 3 = 1 { the strings are = GAT }
So total substrings for string length 3 are = (1 + 2 + 3) + 1
Similarly total substrings for string length n are = (1 + 2 + 3 + ................. n times) + 1 =(n(n+1)/2) + 1
Here substrings of length 0 is excluded.
So total substrings are = (n(n+1)/2).
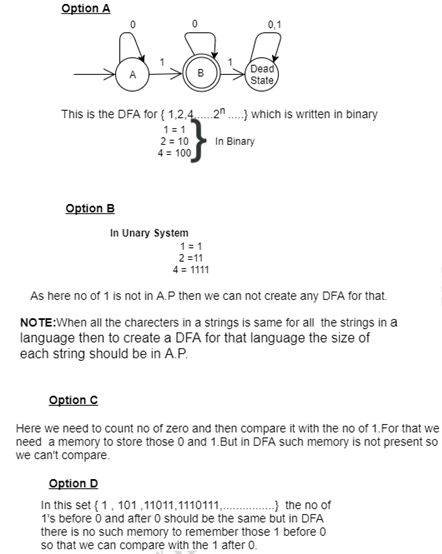
Q35. Which of the following sets can be recognized by a Deterministic Finite-state
Automation?
(a) The numbers 1,2,4,8, ...... 2n, ............. written in binary.
(b) The numbers 1,2,4,..... 2n, ..... written in unary.
(c) The set of binary strings in which the numbers of zeros is the same as the numbers of ones.
(d) The set {1,101,11011,1110111,...}.
Q36. The string 1101 does not belong to the set represented by
(a) 110∗(0+1)
(b) 1(0+1)∗101
(c) (10)∗(01)∗(00+11)∗
(d) (00+(11)∗0)∗
Show Answer
Answer : Option ( C,D )
Q37. If the regular set A is represented by A=(01+1)∗ and the regular set ′B′ is
represented by B=((01)∗1∗), which of the following is true?
(a) A⊂B
(b) B⊂A
(c) A and B are incomparable
(d) A=B
Q38. ∑={a,b}, which one of the following sets is not countable.
(a) Set of all strings over ∑
(b) Set of all languages over ∑
(c) Set of all regular languages over ∑
(d) Set of all languages over ∑ accepted by Turing Machines.
Show Answer
Answer : Option (B)
Explanation:
Only option B is correct as set of all languages are uncountable.
Remember: As set of all Turing Machine are countable.So we can say that
(1) Set of all Recursively Enumerable Language are countable.
(2) Set of all Recursively Language are countable.
(3) Set of all Context-Sensitive Language are countable.
(4) Set of all Context Free Language are countable.
(5) Set of all Regular Language are countable.
Q39. Let L⊆∑∗ where ∑={a,b} which of the following is true?
(a) L={x|x has an equal number of a′s and b′s} is regular
(b) L={a^nb^n|n≥1} is regular
(c) L={x|x has more a′s than b′s} is regular
(d) L={a^mb^n|m≥1,n≥1} is regular
Show Answer
Answer : Option ( D )
Q40. Which two of the following four regular expressions are equivalent?
(i) (00)∗(ε+0)
(ii) (00)∗
(iii) 0∗
(iv) 0(00)∗
(a) (i) and (ii)
(b) (ii) and (iii)
(c) (i) and (iii)
(d) (iii) and (vi)
Show Answer
Answer : Option (C)
Explanation:
0*= { ε ,0,00,000,............}
(00)*(ε+0)= (00)* + (00)*0 = even + odd = 0*
So,0* = (00)*(ε+0)
Q41. State True or False with one line explanation:
A FSM (Finite State Machine) can be designed to add two integers of any arbitrary length (arbitrary number of digits).
(a) TRUE
(b) FALSE
Show Answer
Answer : Option (B)
Explanation: As FSM has a finite memory then it can not store carry bit to add arbitary
length strings.
Q42. Consider the following language.
L = { w ∈ {0, 1}* | w ends with the substring 011}
Which one of the following deterministic finite automata accepts L?
(a) figure 1
(b) figure 2
(c) figure 3
(d) figure 4
Show Answer
Answer : Option ( D )
Q43. Consider the following language.
L = {x ∈ {a, b}* | number of a’s in x is divisible by 2 but not divisible by 3}
The minimum number of states in a DFA that accepts L is ______.
(a) 2
(b) 3
(c) 6
(d) 9
(d) figure 4
Show Answer
Answer : Option ( C )
Q44. Let N be an NFA with n states. Let k be the number of states of a minimal DFA
which is equivalent to N. Which one of the following is necessarily true?
Which one of the following is necessarily true?
(a) k≥2n
(b) k≥n
(c) k≤n2
(d) k≤2n
Show Answer
Answer : Option ( D )
Q45. The number of states in the minimal deterministic finite automaton corresponding to
the regular expression (0+1)∗(10) is ________________.
(a) 1
(b) 2
(c) 3
(d) 4
Show Answer
Answer : Option (C)
Q46. Consider the DFAs M and N given above. The number of states in a minimal DFA
that accepts the language L(M) ∩ L(N) is___________.
(a) 2
(b) 1
(c) 3
(d) 4
Show Answer
Answer : Option (B)
Q47. Consider the NPDA ⟨Q={q0,q1,q2}, Σ={0,1}, Γ={0,1,⊥}, δ,q0,⊥, F={q2}⟩ , where (as per usual convention) Q is the set of states, Σ is the input alphabet, Γ is the stack alphabet, δ is the state transition function q0 is the initial state, ⊥ is the initial stack symbol, and F is the set of accepting states. The state transition is as follows:
Which one of the following sequences must follow the string 101100 so that the overall string is accepted by the automaton?
(a) 10110
(b) 10010
(c) 01010
(d) 01001
Show Answer
Answer : Option (B)
Q48. Let L1={w∈{0,1}∗|w has at least as many occurrences of (110)′s as (011)′s}. Let
L2={w∈{0,1}∗|w has at least as many occurrences of (000)′s as (111)′s}. Which one of
the following is TRUE?
(a) L1 is regular but not L2
(b) L2 is regular but not L1
(c) Both L1 and L2 are regular
(d) Neither L1 nor L2 are regular
Show Answer
Answer : Option (A)
Q49. Let L1={w∈{0,1}∗|w has at least as many occurrences of (110)′s as (011)′s}. Let
L2={w∈{0,1}∗|w has at least as many occurrences of (000)′s as (111)′s}. Which one of
the following is TRUE?
(a) L1 is regular but not L2
(b) L2 is regular but not L1
(c) Both L1 and L2 are regular
(d) Neither L1 nor L2 are regular
Show Answer
Answer : Option (A)
Q50. Which of the regular expression given below represent the following DFA?
(i) 0*1(1+00*1)*
(ii) 0*1*1+11*0*1
(iii) (0+1)∗*1
(a) I and II only
(b) I and III only
(c) II and III only
(d) I, II and III
Show Answer
Answer : Option (B)
Q51. Consider the following languages
L1={0p1q0r|p,q,r≥0}
L2={0p1q0r|p,q,r≥0,p≠r}
Which one of the following statements is FALSE?
(a) L2 is context-free
(b) L1∩L2 is context-free
(c) Complement of L2 is recursive
(d) Complement of L1 is context-free but not regular
Show Answer
Answer : Option ( D )
Q52. Let L={w∈(0+1)∗|w has even number of 1′s}, i.e L is the set of all bit strings with
even number of 1′s. which one of rhe regular expression below represents L.
(a) (0∗10∗1)∗
(b) 0∗(10∗10∗)∗
(c) 0∗(10∗1)∗0∗
(d) 0∗1(10∗1)∗10∗
Show Answer
Answer : Option (B)
Q53. The above DFA accepts the set of all strings over {0,1} that
(a) Begin either with 0 or 1
(b) End with 0
(c) End with 00.
(d) Contain the substring 00.
Show Answer
Answer : Option (C)
Q54. L=L1∩L2 where L1 and L2 are languages defined as follows.
L1={ambmcanbn|m,n≥0}
L2={aibick|i,j,k≥0} Then L is
(a) Not recursive
(b) Regular
(c) Context free but not regular
(d) Recursively enumerable but not context free
Show Answer
Answer : Option ( D )
Q55. Which of the following are regular sets?
(a) I & IV only
(b) I & III only
(c) I only
(d) IV only
Show Answer
Answer : Option (C)
Q56. Which of the following languages is regular?
(a) {ww^R|w∈{0,1}+}
(b) {ww^Rx|x,w∈{0,1}+}
(c) {wxw^R|x,w∈{0,1}+}
(d) {xww^R|x,w∈{0,1}+}
Show Answer
Answer : Option (C)
Q57. Given that language L1 is regular and that the language L1∩L2 is regular is the
language L2 is always regular?
(a) Yes
(b) No
Show Answer
Answer : Option (A)
Q58. Consider the following languages:
L1={ww|w∈{a,b}∗}
L2={a^nb^nc^m|m,n≥0}
L3={a^mb^nc^n|m,n≥0}
Which of the following statements is/are FALSE?
(a) L1 is not context-free but L2 and L2 are deterministic context-free.
(b) Neither L1 nor L2 is context-free.
(c) L2, L3 and L2 ∩ L3 all are context-free.
(d) Neither L1 nor its complement is context-free.
Show Answer
Answer : Option (B, C, D )
Explanation:
L1={ww|w∈{a,b}∗}
L2={anbncm|m,n≥0}
L3={ambncn|m,n≥0}
L1 is not context free because it has string matching in straight order, which PDA cannot do.
L2 and L3 are clearly DCFL's, since they have only one comparison and DPDA can accept both.
(a) is therefore true.
(b) is false since L2 is DCFL and every DCFL is a CFL.
(c) is false because L2 ∩ L3 = {anbncn | n ≥ 0} is not a CFL.
(d) is false because complement of "ww" has CFG and is CFL.
Q59. Consider the following languages:
L1 = {a^nwa^n | w ∈ {a, b}*}
L2 = {wxw^R | w, x ∈ {a, b}*, | w | , | x | > 0}
Note that wR is the reversal of the string w. Which of the following is/are TRUE?
(a) L1 and L2 are regular.
(b) L1 and L2 are context-free
(c) L1 is regular and L2 is context-free.
(d) L1 and L2 are context-free but not regular.
Show Answer
Answer : Option (A, B, C )
Explanation:
L1 = {a^nwa^n | w ∈ {a, b}*}
L2 = {wxw^R | w, x ∈ {a, b}*, | w | , | x | > 0}
L1 is regular because by putting n = 0, we create a subset {w | w∈ {a, b}*} which contains all possible strings. So if subset of L1 is (a + b)*, then L1 = (a b)*.
L2 is regular because by putting w as "a" and "b" we get a regular expression a(a + b)+a + b(a + b)+b, which covers all other string which can be obtained by putting w as "a", "ab", "ba", "bb", etc.
So, L2 = a(a + b)+a + b(a + b)+b, which is regular.
So, L1 and L2 both are regular.
Now every regular is also context-free.
So, option (a), (b), (c) are all true and option (d) is false.
Q60. Consider the language
L = { a^n|n≥0 } ∪ { a^nb^n|n≥0 }
and the following statements.
I. L is deterministic context-free.
II. L is context-free but not deterministic context-free.
III. L is not LL(k) for any k.
Which of the above statements is/are TRUE?
(a) I only
(b) II only
(c) I and III only
(d) III only
Show Answer
Answer : Option (C)
Q61. Which of the following languages is generated by the given grammar?
S→aS|bS|ε
(a) {a^nb^m|n,m≥0}
(b) {w∈{a,b}∗|w has equal number of a′s and b′s}
(c) {a^n|n≥0}∪{b^n|n≥0}∪{a^nb^n|n≥0}
(d) {a,b}∗
Show Answer
Answer : Option ( D )
Q62. The lexical analysis for a modern computer language such as java needs the power
of which one of the following machine model in a necessary and sufficient sense?
(a) Finite state automata
(b) Deterministic pushdown automata
(c) Non -deterministic pushdown automata
(d) Turing machine
Show Answer
Answer : Option (A)
Q63. S→aSa|bSb|a|b
The language generated by the above grammar over the alphabet {a,b} is the set of
(a) All palindromes
(b) All odd length palindromes
(c) Strings that begin and with same symbol
(d) All even length palindromes
Show Answer
Answer : Option (C)
Q64. Which one of the following is FALSE?
(a) There is a unique minimal DFA for every regular language
(b) Every NFA can be converted to an equivalent PDA
(c) Complement of every context free language is recursive
(d) Every non deterministic PDA can be converted to an equivalent deterministic PDA
Show Answer
Answer : Option (B)
Q65. Let L1={0^n+m1^n0^m|n,m≥0},
L2={0^n+m1^n+m0^m|n,m≥0}, and
L3={0^n+m1^n+m0^n+m|n,m≥0}, Which of these languages are NOT context free?
(a) L1 only
(b) L3 only
(c) L1 and L2
(d) L2 and L3
Show Answer
Answer : Option ( D )
Q66. Which of the following grammar rules violate the requirements of an operator
grammar? P, Q,R are non-terminals and r,s,t are terminals.
1)P→QR
2)P→QsR
3)P→c
4)P→QtRr
(a) (1) only
(b) (1) and (3) only
(c) (2) and (3) only
(d) (3) and (4) only
Show Answer
Answer : Option (B)
Q67. The language accepted by a pushdown Automation in which the stack is limited to
10 items is best described as
(a) Context free
(b) Regular
(c) Deterministic Context Free
(d) Recursive
Show Answer
Answer : Option (C)
Q68. Which of the following statement is true?
(a) If a language is context free it can always be accepted by deterministic pushdown
automation
(b) The union of two context free language is context free
(c) The intersection of two context free languages is context free
(d) The complement of a context free language is context free
Show Answer
Answer : Option (B)
Q69. Context free languages are closed under:
(a) Union, intersection
(b) Union, Kleene closure
(c) Intersection, complement
(d) Complement, Kleene Closure
Show Answer
Answer : Option (B)
Q70. Let LD be the set of all languages accepted by a PDA by final state and LE the set
of all languages accepted by empty stack. Which of the following is true?
(a) LD=LE
(b) LD⊃LE
(c) LD⊂LE
(d) None of the above
Show Answer
Answer : Option (A)
Q71. Consider the grammar with the following productions.
S→aαb|bαc|aB
S→αS|b
S→αbb|ab
Sα→bdb|b
the above grammar is
(a) Context free grammar
(b) Regular grammar
(c) Context sensitive grammar
(d) LR(k)
Show Answer
Answer : Option ( D )
Q72. State whether the following statement is TRUE / FALSE. The problem is to whether
a Turing Machine M accepts input w is un-decidable.
(a) TRUE
(b) FALSE
Show Answer
Answer : Option (B)
Q73. State whether the following statement is TRUE / FALSE.
The intersection of two CFL′s is also CFL.
(a) TRUE
(b) FALSE
Show Answer
Answer : Option (B)
Q74. State whether the following statement is TRUE / FALSE.
A is recursive if both a and its complement are accepted by Turing Machine M accepts.
(a) TRUE
(b) FALSE
Show Answer
Answer : Option (B)
Q75. State whether the following statement is TRUE / FALSE.
Regularity is preserved under the operation of string reversal.
(a) TRUE
(b) FALSE
Show Answer
Answer : Option (B)
Q76. State whether the following statement is TRUE / FALSE.
A minimal DFA that is equivalent to an NFDA with n modes has always 2n states
(a) TRUE
(b) FALSE
Show Answer
Answer : Option (B)
Q77. State whether the following statement is TRUE / FALSE.
All subjects of regular sets are regular.
(a) TRUE
(b) FALSE
Show Answer
Answer : Option (B)
Q78. Let ⟨M⟩ denote an encoding of an automation M. Suppose that ∑ = {0, 1}. Which of
the following languages is/are NOT recursive?
(a) L = { ⟨M⟩ | M is a PDA such that L(M) = ∑*}
(b) L = { ⟨M⟩ | M is a DFA such that L(M) = Φ}
(c) L = { ⟨M⟩ | M is a PDA such that L(M) = Φ}
(d) L = { ⟨M⟩ | M is a DFA such that L(M) = ∑*}
Show Answer
Answer : Option (A)
Q79. Consider the following languages.
L1 = {wxyx | w, x, y ∈ (0 + 1)+}
L2 = {xy | x, y ∈ (a + b)*, |x| = |y|, x ≠ y}
Which one of the following is TRUE?
(a) L1 is regular and L2 is context-free.
(b) L1 is context-free but not regular and L2 is context-free.
(c) Neither L1 nor L2 is context-free.
(d) L1 is context-free but L2 is not context-free.
Show Answer
Answer : Option (A)
Q80. Consider the following languages:
I. {a^mb^nc^pd^q|m+p=n+q, where m,n,p,q≥0}
II. {a^mb^nc^pd^q|m=n and p=q, where m,n,p,q≥0}
III. {a^mb^nc^pd^q|m=n=p and p≠q, where m,n,p,q≥0}
IV. {a^mb^nc^pd^q|mn=p+q, where m,n,p,q≥0}
Which of the languages above are context-free?
(a) I and IV only
(b) I and II only
(c) II and III only
(d) II and IV only
Show Answer
Answer : Option (B)
Q81. Consider the following context-free grammars:
G1:S→aS|B,B→b|bBG2:S→aA|bB,A→aA|B|ε,B→bB|ε
Which one of the following pairs of languages is generated by G1 and G2, respectively?
(a) {a^mb^n|m>0 or n>0} and {a^mb^n|m>0 and n>0}
(b) {a^mb^n|m>0 and n>0} and {a^mb^n|m>0 or n≥0}
(c) {a^mb^n|m≥0 or n>0} and {a^mb^n|m>0 and n>0}
(d) {a^mb^n|m≥0 and n>0} and {a^mb^n|m>0 or n>0}
Show Answer
Answer : Option ( D )
Q82. Which of the following languages are context-free?
L1={a^mb^na^nb^m|m,n≥1}
L2={a^mb^na^mb^n|m,n≥1}
L3={a^mb^n|m=2n+1}
(a) L1 and L2 only
(b) L1 and L3 only
(c) L2 and L3 only
(d) L3 only
Show Answer
Answer : Option (B)
Q83. Consider the following languages over the alphabet ∑={0,1,c}:
L1={0^n1^n|n≥0}L2={wcw^r|w∈{0,1}∗}L3={ww^r|w∈{0,1}∗}
Here, w^r is the reverse of the string w. Which of these languages are deterministic
Context- free languages?
(a) None of the languages
(b) (B) Only L1
(c) Only L1 and L2
(d) All the three languages.
Show Answer
Answer : Option (C)
Q84. Consider the DFA A given below.
Which of the following are FALSE?
1. Complement of L(A) is context - free.
2. L(A) =(11∗0+0)(0+1)∗0∗1∗)
3. For the language accepted by A,A is the minimal DFA.
4. A accepts all strings over {0,1} of length at least 2.
(a) 1 and 3 only
(b) 2 and 4 only
(c) 2 and 3 only
(d) 3 and 4 only
Show Answer
Answer : Option ( D )
Q85. Consider the languages
L1={0^i1^j|i≠j}
L2={0^i1^j|i=j}
L3={0^i1^j|i=2j+1}
L4={0^i1^j|i≠2j}
(a) only L2 is context free
(b) only L2 and L3 are context free
(c) only L1 and L2 are context free
(d) all are context free
Show Answer
Answer : Option ( D )
Q86. Match the following List-I with List - II
List-I
E) Checking that identifiers are declared before their
F) Number of formal parameters in the declaration of a function agrees with the number
of actual parameters in a use of that function
G) Arithmetic expression with matched pairs of parentheses
H) Palindromes
List-II
P) L={a^nb^mc^nd^m|n≥1,m≥1}
Q) X→XbX|XcX|dXf|g
R) L={www|w∈(a|b)∗}
S) X→bXB|cXc|ε
(a) E−P,F−R,G−Q,H−S
(b) E−R,F−P,G−S,H−Q
(c) E−R,F−P,G−Q,H−S
(d) E−P,F−R,G−S,H−Q
Show Answer
Answer : Option (C)
Q87. Which of the following statements are true?
1. Every left-recursive grammar can be converted to a right-recursive grammar and viceversa
2. All ε-productions can be removed from any context-free grammar by suitable
transformations
3. The language generated by a context-free grammar all of whose productions are of the
form X→w or X→wY (where, w is a string of terminals and Y is a non terminal), is
always regular
4. The derivation trees of strings generated by a context-free grammar in Chomsky
Normal Form are always binary trees
(a) 1,2,3 and 4
(b) 2,3 and 4 only
(c) 1,3 and 4 only
(d) 1,2 and 4 only
Show Answer
Answer : Option (C)
Q88. Which of the following statement is false?
(a) Every NFA can be converted to an equivalent DFA
(b) Every non-deterministic Turing machine can be converted to an equivalent
deterministic Turing machine.
(c) Every regular language is also a context- free language
(d) Every subset of a recursively enumerable set is recursive
Show Answer
Answer : Option ( D )
Q89. Consider the CFG with {S,A,B} as the non-terminal alphabet, {a,b} as the terminal
alphabet, S as the start symbol and the following set of production rules:
Which of the following strings is generated by the grammar?
(a) aaaabb
(b) aabbbb
(c) aabbab
(d) abbbba
Show Answer
Answer : Option (C)
Q90. The language L={0^i21^i|i≥0} over the alphabet {0,1,2} is
(a) Not recursive.
(b) is recursive and is a deterministic CFL.
(c) is a regular language.
(d) is not a deterministic CFL but a CFL.
Show Answer
Answer : Option (B)
Q91. Consider the CFG with {S,A,B} as the non-terminal alphabet, {a,b} as the terminal
alphabet, S as the start symbol and the following set of production rules:
For the correct string of (earlier question) how many derivation trees are there?
(a) 1
(b) 2
(c) 3
(d) 4
Show Answer
Answer : Option (B)
Q92. Consider the following statements about the context-free grammar
G={S→SS,S→ab,S→ba,S→ε}
1. G is ambiguous
2. G produces all strings with equal number of a′s and b′s
3. G can be accepted by a deterministic PDA.
Which combination below expresses all the true statements about G?
(a) 1 only
(b) 1 and 3 only
(c) 2 and 3 only
(d) 1,2 and 3
Show Answer
Answer : Option ( D )
Q93. Consider the language :
L1={ww^R|w∈{0,1}∗}
L2={w≠w^R|w∈{0,1}∗} where ≠ is a special symbol
L3={ww|w∈{0,1}∗}
Which one of the following is TRUE?
(a) L1 = is a deterministic CFL
(b) L2 = is a deterministic CFL
(c) L3 is a CFL, but not a deterministic CFL
(d) L3 IS A DETERMINISTIC CFL
Show Answer
Answer : Option (B)
Q94. Consider the language :
L1={a^nb^nc^m|n,m>0} and L2={a^nb^mc^m|n,m>0}
Which of the following statement is FALSE?
(a) L1∩L2 is a context-free language
(b) L1∩L2 is a context-free language
(c) L1 and L2 are context-free language
(D) L1∩L2 is a context sensitive language
Show Answer
Answer : Option ( D )
Q95. Let M=(K,∑,F,Δ,s,F) be a pushdown automation. Where K={s,f},F={f},∑={a,b},F={a} and Δ={((s,a,∈),(s,a)),((s,b,∈),(s,a)), ((s,a,∈),(f,∈),((f,a,a),(f,∈)),((f,b,a),(f,∈))}.
Which one of the following strings is not a number of L(M)?
(a) aaa
(b) aabab
(c) baaba
(d) bab
Show Answer
Answer : Option (C)
Q96. The language {a^mb^nc^m+n|m,n≥} is
(a) Regular
(b) Context-free but not regular
(c) Context sensitive but not context free
(d) Type-0 but not context sensitive
Show Answer
Answer : Option (B)
Q97.Consider the following grammar G:
S→bS|aA|bA→bA|aBB→bB|aS|a
Let Na(w) and Nb(w) denote the number of a′s and b′s in a string w respectively. The
language
L(G)⊆{a,b}+ generated by G is
(a) {w|Na(w)>3Nb(w)}
(b) {w|Nb(w)>3Na(w)}
(c) {w|Na(w)=3k,k∈{0,1,2,...}}
(d) {w|Nb(w)=3k,k∈{0,1,2,...}}
Show Answer
Answer : Option (C)
Q98. Consider the following decision problems:
P1 Does a given finite state machine accept a given string
P2 Does a given context free grammar generate an infinite number of stings.
Which of the following statements is true?
(a) Both P1 and P2 are decidable
(b) Neither P1 and P2 are decidable
(c) Only P1 is decidable
(d) Only P2 is decidable
Show Answer
Answer : Option (A)
Q99. If L1 is a context free language and L2 is a regular which of the following is/are
false?
(a) L1−L2 is not context free
(b) L1∩L2 is context free
(c) ∼L1 is context free
(d) ∼L2 is regular
Show Answer
Answer : Option (A, C )
Q100. Which of the following statements is false?
(a) Every finite subset of a non-regular set is regular
(b) Every subset of a regular set is regular
(c) Every finite subset of a regular set is regular
(d) The intersection of two regular sets is regular
Show Answer
Answer : Option (B)
Q101. Let L be the set of all binary strings whose last two symbols are the same. The
number of states in the minimum state deterministic finite-state automation accepting L is
(a) 2
(b) 4
(c) 5
(d) 8
Show Answer
Answer : Option (C)
Q102. Which of the following languages over {a,b,c} is accepted by Deterministic push
down automata?
(a) {w⊂w^R|w∈{a,b}∗}
(b) {ww^R|w∈{a,b,c}∗}
(c) {a^nb^nc^n|n≥0}
(d) {w|w is palindrome over {a,b,c}}
Show Answer
Answer : Option (A)
Q103. If L1 and L2 are context free languages and R a regular set, one of the languages
below is not necessarily a context free language. Which one?
(a) L1L2
(b) L1∩L2
(c) L1∩R
(d) L1∪L2
Show Answer
Answer : Option (B)
Q104. Which of the following features cannot be captured by context-free grammars?
(a) Syntax of if-then-else statements
(b) Syntax of recursive procedures
(c) Whether a variable has been declared before its use
(d) Variable names of arbitrary length
Show Answer
Answer : Option (C)
Q105. Context-free languages are
(a) closed under union
(b) closed under complementation
(c) closed under intersection
(d) closed under Kleene closure.
Show Answer
Answer : Option (A, D )
Q106. Context free languages and regular languages are both closed under the
operation(s) of :
(a) Union
(b) Intersection
(c) Concatenation
(d) Complementation
Show Answer
Answer : Option (A, C )
Q107. FORTRAN is:
(a) Regular language.
(b) Context free language.
(c) Context sensitive language.
(d) None-of the above.
Show Answer
Answer : Option (C)
108. A context-free grammar is ambiguous if:
(a) The grammar contains useless non-terminals.
(b) It produces more than one parse tree for some sentence.
(c) Some production has two non-terminals side by side on the right-hand side.
(d) None of the above.
Show Answer
Answer : Option (B)
Q109. Which of the following is/are undecidable?
(a) Given two Turing machines M1 and M2, decide if L(M1) = L(M2).
(b) Given a Turing machine M, decide if L(M) is regular.
(c) Given a Turing machine M, decide if M accepts all strings.
(d) Given a Turing machine M, decide if M takes more than 1073 steps on every string.
Show Answer
Answer : Option (A, B, C )
Explanation:
A, B, C choices are all non-trivial properties of RE language (language of TM's) and
hence all UNDECIDABLE.
Choice (d) is DECIDABLE. Why?
A Turing Machine see only at most the first 1073 symbols of input in its first 1073 steps.
Hence whether it stops on first 1073 steps depends only on the first 1073 symbols of input.
Since the number of strings of length 1073 is finite, it gives a way to decide this. Run the input machine M on all inputs of length 1073 and check whether any of them stops within 1073 steps. If so, reject, otherwise accept.
Q110. Which of the following statements is/are TRUE?
(a) Every subset of a recursively enumerable language is recursive.
(b) If a language L and its complement L― are both recursively enumerable, then L
must be recursive.
(c) Complement of a context-free language must be recursive.
(d) If L1 and L2 are regular, then L1 ∩ L2 must be deterministic context-free.
Show Answer
Answer : Option (B, C, D )
Explanation:
(a) No language is closed under subset operation. So subset of an RE language may or may not be REC. So option (a) is false.
(b) If L and L― are both RE ⇒ L is REC is a theorem and is true.
(c) (CFL)C = (CSL)C = CSL
Every CSL is recursive.So, complement of CFL is recursive is true.
(d) L1 → regular, L2 → regular
⇒ L1 ∩ L2 = Regular ∩ Regular = Regular
Now every regular language is a DCFL.
So, option (d) is true.
Q111. Consider the following types of languages: L1: Regular, L2: Context-free, L3: Recursive, L4: Recursively enumerable. Which of the following is/are TRUE?
I. L3'―∪L4 is recursively enumerable
II. L2'―∪L3 is recursive
III. L1∗∩L2 is context-free
IV. L1∪L2'― is context-free
(a) I only
(b) I and III only
(c) I and IV only
(d) I, II and III only
Show Answer
Answer : Option ( D )
Q112. Consider the following statements.
I. The complement of every Turing decidable language is Turing decidable
II. There exists some language which is in NP but is not Turing decidable
III. If L is a language in NP, L is Turing decidable
Which of the above statements is/are true?
(a) Only II
(b) Only III
(c) Only I and II
(d) Only I and III
Show Answer
Answer : Option ( D )
Q113. For any two languages L1 and L2 such that L1 is context-free and L2 is recursively
enumerable but not recursive, which of the following is/are necessarily true?
I. L'―1 (complement of L1) is recursive
II. L'―2 (complement of L2) is recursive
III. L'―1 is context-free
IV. L'―1∪L2 is recursively enumerable
(a) I only
(b) III only
(c) III and IV only
(d) I and IV only
Show Answer
Answer : Option ( D )
Q114. Let A≤mB denotes that language A is mapping reducible (also known as many-toone reducible) to language B. Which one of the following is FALSE?
(a) If A≤mB and B is recursive then A is recursive.
(b) If A≤mB and A is undecidable then B is un-decidable.
(c) If A≤mB and B is recursively enumerable then A is recursively enumerable.
(d) If A≤mB and B is not recursively enumerable then A is not recursively enumerable.
Show Answer
Answer : Option ( D )
Q115. Which of the following statements is/are FALSE?
1. For every non-deterministic Turing machine, there exists an equivalent deterministic Turing machine
2. Turing recognizable languages are closed under union and complementation
3. Turing decidable languages are closed under intersection and complementation
4. Turing recognizable languages are closed under union and intersection
(a) 1 and 4 only
(B) 1 and 3 only
(c) 2 only
(d) 3 only
Show Answer
Answer : Option (C)
Q116. Which of the following is true for the language {a^p|P prime }?
(a) It is not accepted by a Turing machine
(b) It is regular but not context-free
(c) It is context-free but not regular
(d) It is neither regular nor context-free, but accepted by a Turing machine
Show Answer
Answer : Option ( D )
Q117. If the strings of a language L can be effectively enumerated in lexicographic (i.e., alphabetic(c) order, which of the following statements is true?
(a) L is necessarily finite
(b) L is regular but not necessarily finite
(C) L is context free but not necessarily regular
(d) L is recursive but not necessarily context free
Show Answer
Answer : Option ( D )
Q118. Regarding the power of recognition of languages, which of the following statement is false?
(a) The non-deterministic finite-state automata are equivalent to deterministic finite-state automata.
(b) Non-deterministic Push-down automata are equivalent to deterministic Pushdown automata.
(c) Non-deterministic Turing machines are equivalent to deterministic Turing machines.
(d) Multi-tape Turing machines are equivalent to Single-tape Turing machines.
Show Answer
Answer : Option (B)
Q119. Which of the following statements is / are true / false?
Regular languages are closed under infinite union.
(a) TRUE
(b) FALSE
Show Answer
Answer : Option (B)
Q120. Which of the following statements is / are true / false?
Union of two recursive languages is recursive
(a) TRUE
(b) FALSE
Show Answer
Answer : Option (B)
Q121. Which of the following statements is / are true / false?
The language {0^n|n is prime} is not regular
(a) TRUE
(b) FALSE
Show Answer
Answer : Option (B)
Q122. For a Turing machine M, {M} denotes an encoding of M. Consider the following
two languages.
L1 = {(M) | M takes more than 2021 steps on all inputs}
L2 = {(M) | M takes more than 2021 steps on some input}
Which one of the following options is correct?
(a) Both L1 and L2 are undecidable.
(b) L1 is undecidable and L2 is decidable.
(c) L1 is decidable and L2 is undecidable.
(d) Both L1 and L2 are decidable.
Show Answer
Answer : Option ( D )
Q123. Consider the following problems. L(G) denotes the language generated by a grammar G. L(M) denotes the language accepted by a machine M.
I. For an unrestricted grammar G and a string W, whether w∈L(G)
II. Given a Turing machine M, whether L(M) is regular
III. Given two grammars G1 and G2, whether L(G1)=L(G2)
IV. Given an NFA N, whether there is a deterministic PDA P such that N,and P accept the same language.
Which one of the following statements is correct?
(a) Only I and II are undecidable
(b) Only III is undecidable
(c) Only II and IV are undecidable
(d) Only I, II and III are undecidable
Show Answer
Answer : Option ( D )
Q124. The set of all recursively enumerable languages is
(a) closed under complementation.
(b) closed under intersection.
(c) a subset of the set of all recursive languages
(d) an uncountable set.
Show Answer
Answer : Option (B)
Q125. Consider the following languages.
L1={⟨M⟩|M takes at least 2016 steps on some input },
L2={⟨M⟩|M takes at least 2016 steps on all inputs } and
L3={⟨M⟩|M accepts ε},
where for each Turing machine M,⟨M⟩ denotes a specific encoding of M. Which one of the following is TRUE?
(a) L1 is recursive and L2,L3 are not recursive
(b) L2 is recursive and L1,L3 are not recursive
(c) L1,L2 are recursive and L3 is not recursive
(d) L1,L2,L3 are recursive
Show Answer
Answer : Option (C)
Q126. Let X be a recursive language and Y be a recursively enumerable but not recursive language. Let W and Z be two languages such that Y'― reduces to W, and Z reduces to X'― (reduction means the standard many-one reduction). Which one of the following statements is TRUE?
(a) W can be recursively enumerable and Z is recursive.
(B) W can be recursive and Z is recursively enumerable.
(c) W is not recursively enumerable and Z is recursive.
(d) W is not recursively enumerable and Z is not recursive.
Show Answer
Answer : Option (C)
Q127. Let L be a language and L'― be its complement. Which one of the following is NOT a viable possibility?
(a) Neither L nor L'― is recursively enumerable (r.e).
(b) One of L and L'― is r.e. but not recursive; the other is not r.e.
(c) Both L and L'― are r.e. but not recursive.
(d) Both L and L'― are recursive.
Show Answer
Answer : Option (C)
Q128. Let <M> be the encoding of a Turing machine as a string over ∑={0,1}.
Let L={<M>|M is a Turing machine that accepts a string of length 2014}. Then, L is
(a) decidable and recursively enumerable
(b) un-decidable but recursively enumerable
(c) un-decidable and not recursively enumerable
(d) decidable but not recursively enumerable
Show Answer
Answer : Option (B)
Q129. If L and L'― are recursively enumerable then L is
(a) Regular
(b) Context-free
(c) Context-sensitive
(d) Recursive.
Show Answer
Answer : Option ( D )
Q130. Let L1 be a regular language, L2 be a deterministic context-free language and L3 a
recursively enumerable, but not recursive, language. Which one of the following
statement is false?
(a) L1∩L2 is deterministic CFL
(b) L3∩L1 is recursive
(c) L1∪L2 is context-free
(d) L1∩L2∩L3 is recursively enumerable
Show Answer
Answer : Option (B)
Q131. For s∈(0+1)∗, let d(s) denote the decimal value of s(e.g.d(101)=5)
Let L={s∈(0+1)∗|d(s) mod 5=2 and d(s) mod 7≠4}
Which of the following statement is true?
(a) L is recursively enumerable, but not recursive
(b) L is recursive, but not context-free
(c) L is context-free, but not regular
(d) L is regular
Show Answer
Answer : Option ( D )
Q132. Let L1 be a recursive language, and Let L2 be a recursively enumerable but not a
recursive language. Which one of the following is TRUE?
(a) L1'― is recursive and L2'― is recursively enumerable
(b) L1'― is recursive and L2'― is not recursively enumerable
(c) L1'― and L2― are recursively enumerable
(d) L1'― is recursively enumerable and L2'― is recursive
Show Answer
Answer : Option (B)
Q133. The C language is:
(a) A context free language
(b) A context sensitive language
(c) A regular language
(d) Parsable fully only by a Turing machine
Show Answer
Answer : Option (A)
Q134. Which of the following is true?
(a) The complement of a recursively language is recursive.
(b) The complement of a recursively enumerable language is recursively enumerable.
(c) The complement of a recursively language is either recursive or recursively enumerable.
(d) The complement of a context-free language is context-free.
Show Answer
Answer : Option (C)
Q135. Which one of the following is not decidable?
(a) Given a Turing machine M, a stings s and an integer k, M accepts s within k steps
(b) Equivalence of two given Turing machines
(c) Language accepted by a given finite state machine is not empty
(d) Language generated by a context free grammar is non empty
Show Answer
Answer : Option (B)
Q136. hich of the following conversions is not possible (algorithmically)?
(a) Regular grammar to context free grammar
(b) Non-deterministic FSA to deterministic FSA
(c) Non-deterministic PDA to deterministic PDA
(d) Non-deterministic Turing machine to deterministic Turing machine
Show Answer
Answer : Option (C)
Q137. In which of the cases stated below is the following statement true?
“For every non-deterministic machine M1 there exists an equivalent deterministic machine M2 recognizing the same language“.
(a) M1 is nondeterministic finite automation
(b) M1 is a nondeterministic PDA
(c) M1 is a non-deterministic Turing machine
(d) For no machine M1 use the above statement true
Show Answer
Answer : Option (A, C )
Q138. Recursive languages are:
(a) A proper superset of context free languages.
(b) Always recognizable by pushdown automata.
(c) Also called Type (0) languages.
(d) Recognizable by Turing machines.
Show Answer
Answer : Option ( D )
Q139. There are ________ tuples in finite state machine.
(a) 4
(b) 5
(c) 6
(d) unlimited
Show Answer
Answer : Option (B)
Explanation: States, input symbols, initial state, accepting state and transition function.
Q140. Finite State transition function maps.
(a) Σ * Q -> Σ
(b) Q * Q -> Σ
(c) Σ * Σ -> Q
(d) Q * Σ -> Q
Show Answer
Answer : Option ( D )
Explanation: Inputs are state and input string output is states.
Q141. Number of states require to accept string ends with 10.
(a) 3
(b) 2
(c) 1
(d) can’t be represented.
Show Answer
Answer : Option (A)
Explanation: This is minimal finite automata.
Q142. Finite State Extended transition function is .
a) Q * Σ* -> Q
b) Q * Σ -> Q
c) Q* * Σ* -> Σ
d) Q * Σ -> Σ
Show Answer
Answer : Option (A)
Explanation: This takes single state and string of input to produce a state.
Q143. Language of finite automata is.
a) Type 0
b) Type 1
c) Type 2
d) Type 3
Show Answer
Answer : Option ( D )
Explanation: According to Chomsky classification.
Q144. Finite automata requires minimum _______ number of stacks.
a) 1
b) 0
c) 2
d) None of the mentioned
Show Answer
Answer : Option (B)
Explanation: Finite automata doesn’t require any stack operation.
Q145. Regular expressions are closed under
a) Union
b) Intersection
c) Kleen star
d) All of the mentioned
Show Answer
Answer : Option ( D )
Q146. Suppose that L1 is a regular and L2 is a context-free language, Which one of the
following languages is NOT necessarily context-free?
(a) L1 ⋅ L2
(b) L1 ∪ L2
(c) L1 ∩ L2
(d) L1 - L2
Show Answer
Answer : Option ( D )
Quick Revision
PDA Tuple
Finite Automata Tuple
Grammars
Context Free Grammar (CFG)
Context Free languages (CFL)
Deterministic Finite Automata (DFA)
Linear Bound Automata (LBA)
Turing Machine (TM)
Finite Automata: It is used to recognize patterns of specific type input. It is the most restricted type of automata which can accept only regular languages (languages which can be expressed by regular expression using OR (+), Concatenation (.), Kleene Closure(*) like a*b*, (a+b) etc.)
Deterministic FA and Non-Deterministic FA: In deterministic FA, there is only one move from every state on every input symbol but in Non-Deterministic FA, there can be zero or more than one move from one state for an input symbol.
Note:
• Language accepted by NDFA and DFA are same.
• Power of NDFA and DFA is same.
• No. of states in NDFA is less than or equal to no. of states in equivalent DFA.
• For NFA with n-states, in worst case, the maximum states possible in DFA is 2n
• Every NFA can be converted to corresponding DFA.
Identities of Regular Expression :
Φ + R = R + Φ = R
Φ * R = R * Φ = Φ
ε * R = R * ε = R
ε* = ε
Φ* = ε
ε + RR* = R*R + ε = R*
(a+b)* = (a* + b*)* = (a* b*)* = (a* + b)* = (a + b*)* = a*(ba*)* = b*(ab*)*
Moore Machine: Moore machines are finite state machines with output value and its output depends only on present state.
Mealy Machine: Mealy machines are also finite state machines with output value and its output depends on present state and current input symbol.
Push Down Automata: Pushdown Automata has extra memory called stack which gives
more power than Finite automata. It is used to recognize context free languages.
Deterministic and Non-Deterministic PDA: In deterministic PDA, there is only one move from every state on every input symbol but in Non-Deterministic PDA, there can be more than one move from one state for an input symbol.
Note:
• Power of NPDA is more than DPDA.
• It is not possible to convert every NPDA to corresponding DPDA.
• Language accepted by DPDA is subset of language accepted by NPDA.
• The languages accepted by DPDA are called DCFL (Deterministic Context Free
Languages) which are subset of NCFL (Non Deterministic CFL) accepted by NPDA.
Linear Bound Automata: Linear Bound Automata has finite amount of memory called tape which can be used to recognize Context Sensitive Languages.
LBA is more powerful than Push down automata.
FA < PDA < LBA < TM
Turing Machine: Turing machine has infinite size tape and it is used to accept Recursive
Enumerable Languages.
Turing Machine can move in both directions. Also, it doesn’t accept ε .If the string inserted in not in language, machine will halt in non-final state.
Deterministic and Non-Deterministic Turing Machines: In deterministic turing
machine, there is only one move from every state on every input symbol but in NonDeterministic turing machine, there can be more than one move from one state for an
input symbol.
Note:
• Language accepted by NTM, multi-tape TM and DTM are same.
• Power of NTM, Multi-Tape TM and DTM is same.
• Every NTM can be converted to corresponding DTM.
Decidable and Undecidable Problems:
A language is Decidable or Recursive if a Turing machine can be constructed which
accepts the strings which are part of language and rejects others. e.g.; A number is prime
or not is a decidable problem.
A language is Semi–Decidable or Recursive Enumerable if a turing machine can be
constructed which accepts the strings which are part of language and it may loop forever
for strings which are not part of language.
A problem is undecidable if we can’t construct an algorithms and Turing machine which
can give yes or no answer. e.g.; Whether a CFG is ambiguous or not is undecidable.
Countability : Set of all strings over any finite alphabet are countable. Every subset of countable set is either finite or countable.Set of all Turing Machines are countable.The set of all languages that are not recursive enumerable is Uncountable.